接触角测量：方法和应用
接触角是指当一液体与固体表面相接触时，液体在与固体表面相接触（点）处（三相接触边界，3PCP）其液/气-界面形状走向的切线与固体表面（包括液体相一侧）之间的夹角（图-1，-2）。这一角度的值标志着液体在固体表面的润湿性：当润湿性很好时，液体可以在固体表面完全铺展开，呈现0°的接触角值；当润湿性很差时，液体在固体表面完全无法铺展，只能聚集在一起而包成一团，呈现180°的接触角值；当润湿性界于很好与很差之间时，液体在固体表面可以有限度地铺展开来，形成介于 0° ~ 180° 之间的接触角。这一有限的接触角值是体系中各个不同的相互作用力的平衡，也是体系趋向最低能量的结果。涉及的相互作用力包括
液体自身的表面张力（\(\gamma_L\)）：这一值越大，液体越倾向于聚集在一起、包成一团，而不愿意在固体表面上铺展开来；
固体自身的表面张力或表面（自由）能（\(\gamma_S\)）：这一值越大，固体表面的能量位越高，越希望有能量较低的液体层能够在其上面铺展开来而覆盖它，以降低体系的能量；
液体/固体表面-界面的相互作用力（\(\gamma_{SL}\)）：这一值越小，固体表面对液体的吸引力越大，液体越能够在其上面铺展开来，导致较低的接触角值。
所以，如果希望液体能够较好地润湿固体表面：液体的表面张力值越低、固体的表面能值越高、液体/固体表面-界面的相互作用力越强就越有利。
反之，如果希望液体最好不要润湿固体表面：液体的表面张力值越高、固体的表面能值越低、液体/固体表面-界面的相互作用力越弱就越有可能。
如果假设液体的表面张力值（\(\gamma_L\)）是已知的（这一值可以直接测量，所以比较容易准确获得）；如果再假设，\(\gamma_{SL}\) 与 \(\gamma_S\)、\(\gamma_L\) 之间存在某一确定的依赖关系，如 $$ \gamma_{SL} = f\left(\gamma_S, \gamma_L\right) $$
那么接触角的值，\(\theta\)，与这些相互作用力之间的关系，可以表达为： $$ \begin{align} \theta &= g\left(\gamma_S, \gamma_L, \gamma_{SL}\right) \\ &= g\left(\gamma_S, \gamma_L, f\left(\gamma_S, \gamma_L\right)\right) \\ &= h\left(\gamma_S, \gamma_L\right) \end{align} $$
也就是说，接触角的值与液体表面张力和固体表面能有关（上式中的 \(f\)，\(g\) 和 \(h\) 均表示一定的函数/依赖关系）。当前者给定时，其值直接与固体表面能相关。所以测量所使用的液体也被称为探针液体（probe），通过测量它在固体表面的接触角值，可以用来探测固体表面的表面能值，也即固体表面的润湿属性，而这也正是接触角测量之应用基础。
接触角值的测量目前有二种常用的方法：基于称量的Modified Wilhelmy Plate方法 和基于液面（liquid meniscus）形状分析的光学法。前者属于间接的方法，后者属于直接方法。
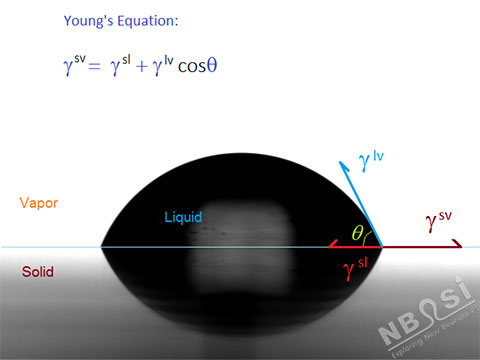图-1：在固体表面上的液滴（座滴）和接触角
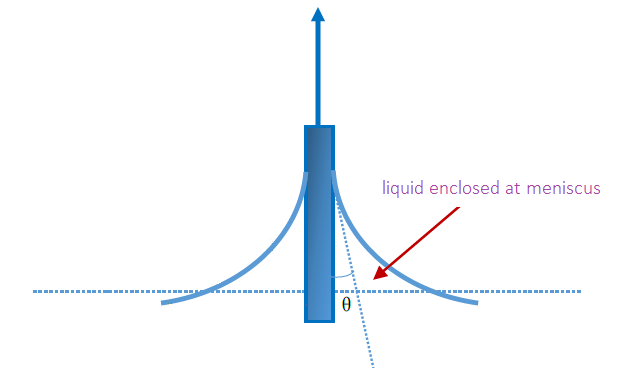图-2：在固体表面上的液面和接触角
Modified Wilhelmy Plate方法
这一方法是在传统的Wilhemy Plate测量液体表面张力方法的基础上发展而来，所以称为modified （经改变的）。
传统的Wilhemy Plate方法被用来测量液体的表面张力：当一块/片规则的金属薄板/片，在经过表面粗糙化处理后，被伸入到液体相时，它受到液体表面张力对其施加的作用力 F（参见图-3）的作用，后者可以通过称量确定。
$$ \gamma = \frac{F}{l\cdot\cos\theta} $$
这里 \(\gamma\) 为液体的表面张力（待测量），\(l\) 为液体润湿金属薄板的总周长（可以通过测量已知表面张力的液体确定或直接通过对薄板几何尺寸的测量经计算获得），\(\theta\) 是液体在薄板表面的接触角值。测量时，假设接触角值为零，可以通过获得的 \(F\) 值由上式计算出 \(\gamma\) 值。
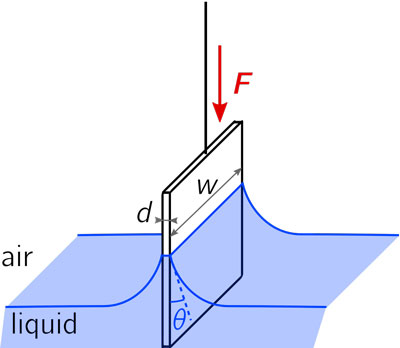图-3：Wilhemy Plate法测量原理示意图
(picture source: https://en.wikipedia.org/wiki/Wilhelmy_plate)
在测量接触角时，把上面的公式转换成以下的形式：$$ \cos\theta = \frac{F}{l\cdot\gamma} $$
通过测量获得的作用力 \(F\)，在已知液体的表面张力值，\(\gamma\)，和液体润湿总周长，\(l\)，时，可以计算得到接触角值 \(\theta\)。
测量时，把待测的样品表面代替金属薄板悬挂在天平的力传感器上，让其缓慢地伸入液体相，记录作用力的变化，由此可以计算获得液体在固体表面的前进接触角值。然后再缓慢地将固体样品从液体相中拉出，记录作用力的变化，由此可以计算获得液体在固体表面的后退接触角值。
所以这一方法可以用来测量液体在固体表面的动态接触角，包括前进和后退接触角值，而且可以很好地控制液体/气体/固体表面-三相接触线的移动速度。
原则上，经改变的Wilhemy Plate法可以用来测量任何几何形状的表面，如果我们可以准确测量其和液体润湿时的总周长 \(l\)，而且这一值在样品移动过程中保持不变（或者我们可以预先知道其变化函数关系）。计算得到的接触角值代表顺着这一润湿总周长的的（平均）有效值。
但是这里遇到这样几个问题：
对于具有不规则形貌的样品表面，其实很难确定/测量其润湿时的总周长 \(l\) ，所以这一方法的测量一般只限于几何形状规则的样品表面，如薄板/片，圆柱体等。当样品表面不平整（如存在较显著的粗糙度、高低起伏，不规则或间隙等）时，这一总周长 \(l\) 的确定也非易事，而这一数值的不确定性，直接地影响到获得的接触角值的可靠性。
计算得到的接触角值代表沿着这一润湿总周长的（平均）有效值。这就要求接触角在这一总周长沿线的值符合一定的分布的（如Gauss分布），而且是相互关联的，否则得到的（平均）有效值缺乏一定的物理意义。比如，如果样品二面的表面属性不同、毫不相干，那么测量得到的液体在二个不同表面上的接触角的（平均）有效值就没有一定的物理意义。这就要求沿着润湿总周长的表面属性是相同的或属于同一类的（也即样品具有相同的二面）。对于实际中的许多样品表面，其实其二面的属性往往是（完全）不相同的，要求测量的也只限于其中的一面（如经过改性的一面） ，虽然有人建议可以把这样的表面通过双面胶带粘结在一起，使得曝露在外的二个表面均是样品需要测量的一面；但在实际操作中，这往往需要时间和耐性，而且也会引入其它的测量误差。
另外，这一方法也要求样品在（上下）移动方向上也基本是均一的，否则测量得到的接触角值很难与具体的样品位置相关联。这就限制了对不均一样品（比如PCB板）进行测量的可能性。
这一方法能够接纳的样品尺寸是非常有限制的：既不能太大，也不能太小。实际遇到的样品尺寸一般都要么太大需要进行切割后才能测量（而这又会带来问题和引入误差）；要么太小，无法进行测量。
再者这一方法在计算时，忽略了样品的边缘（edges）可能对测量和计算的影响，而这是否合理，目前不是非常清楚。
所以这一方法通常只用来测量表面四周属性相同的薄板/薄片和圆柱体（包括纤维）。虽然这一方法也有被用来测量颗粒/粉末的接触角（通过将颗粒/粉末粘结在双面胶带的二面），但在这种情况下，如何测量其润湿时的总周长 \(l\)，是有待进一步商榷的，因为颗粒/粉末组成的表面是不平整的，包括起伏和间隙，其真实的 \(l\) 值可能要比运用几何规则通过简单测量/计算得到的值大得多，这（一疑点）也同样适用于具有微观/纳米表面结构的样品表面。而对于超疏水性表面，这一问题可能更加复杂。
随着样品的移动，测量得到的力（以及计算得到的接触角值）可能随样品的位置而变化，每一时刻的力和接触角值都表示此时沿着润湿总周长的（平均）有效值，所以这一方法可以被用来对样品进行一维扫描（垂直方向）（但如上面已经提及，样品表面必须基本上是均匀的）。
方法的优点在于其测量过程基本上完全自动化（可以减少人为因素的影响），这可以提高测量过程的可重复性。但也必须指出，许多时候润湿总周长 \(l\) 的测量还是无法完全排除操作人员的主观因素。另外，随着基于座滴法的光学接触角直接测量法的自动化程度的不断提高，经改变的Wilhemy Plate法在这方面所具有的优势也越来越不再突出。（前进接触角/后退接触角/接触角滞后性的全自动测量）
基于座滴分析的视频光学接触角测量法
这一方法是通过对在固体表面形成的液体座滴（sessile drop）形状的直接观测、分析和计算来获得接触角的值（参见图-1）。相比于上面的基于改变的Wilhemy Plate称量法，这是一种直接的测量方法。与后者相比，座滴分析测量法适用范围广，灵活性高，更适合用来测量几乎在任何固体表面上的接触角。而且，由于是一种直接测量法，所涉及的假设也比较少。随着座滴分析测量法的自动化程度的不断提高（自动实现液滴在表面的形成，自动确定液滴的三相接触基线位置，自动检测液滴的轮廓坐标，自动对得到的轮廓坐标进行分析和计算等），这一方法即使在人为主观因素可能对测量带来的影响程度上，也不再比基于改变的Wilhemy Plate称量法来得显著。
有关的方法原理请参见下面的专文：
内凹表面接触角测量法
当需要测量的固体表面是一内凹表面时（比如锅底、器皿等容器的内底表面，镜片的凹面等），或者需要测量的位置由于周围有隆起（凸起）的障碍而无法运用通常的侧面座滴法进行测量时，可以采用基于俯视的座滴分析法（俯视法 Top-View）。俯视法不但非常适用于这类表面的测量，而且拥有许多独特的优势，具体请参见下面的专文：
基于其它液面形状分析的视频光学接触角测量法
除了基于液体座滴（sessile drop）形状分析的接触角测量法之外，还有基于对其它的液面形状（liquid meniscus）或构造（configurations）进行分析的接触角测量法。这些液面形状或构造包括：
基于Wilhemy Plate 液面形状的光学分析法；
基于Drop-on-Filiament 的液面形状的光学分析法；
基于Lamella 或 Liquid Bridge 的液面形状的光学分析法；
我们将在以后就这些光学分析法再作叙述和讨论。
参考文献：
M. Müller, C. Oehr, Comments on ‘‘An Essay on Contact Angle Measurements’’ by Strobel and Lyons, Plasma Process. Polym. 2011, 8, 19–24
R. D. Mundo, F. Palumbo, Comments Regarding ‘An Essay on Contact Angle Measurements’, Plasma Process. Polym. 2011, 8, 14–18
© 宁波新边界科学仪器有限公司版权所有，未经许可，禁止转载。