视频光学法接触角测量及原理
测量液体在固体表面接触角一般有二种方法：天平称量法和光学法。
天平称量法是一间接测量法，是薄板法表面张力测量仪的副产物。这一方法只适用于几何形状规则的固体表面（如圆柱体和长方形薄板），而且测量的也只能是整个接触周边表面（periphery of the wetted surface）上的平均接触角值，不能只限于测量其中的一个面。
光学法是建立在直接观测液滴在固体表面的接触界面的测量法，是一种直接测量法。它几乎不受固体表面几何形状和尺寸的限制，适用性广，测量模式众多，而且测量多可在与实际应用相同或相似的条件下进行。自从引入了相机和数字图像处理后，视频光学法不但大大提高了测量的自动化程度和速度，减少了人为主观因素的影响，而且使得测量的精度和准确性也获得大幅度提高。
所有的测量方法都是建立在某一模型的基础上，视频光学法也不例外。如上所述，本法是通过直接观测液体在固体表面形成的液滴的测量法，通过测量液滴的形状，尤其是其与固体表面相接触处（界面）的液面（interface meniscus）形状，来确定液体在固体表面的接触角（参见图1）。基于侧面（side-view）观察法的视频光学法都采用正交观测法（也即从正侧面观测液滴和液面的形状），观测到的只是通过液滴正中轴线的一截面（orthogonal cross section），所以测量方法在一定程度上是默认了液滴和液面的中心轴对称性（rotational invariance），认为从某一旋转角截面测量得到的接触角也同样地可以代表所有的不同取向（旋转角）的截面。
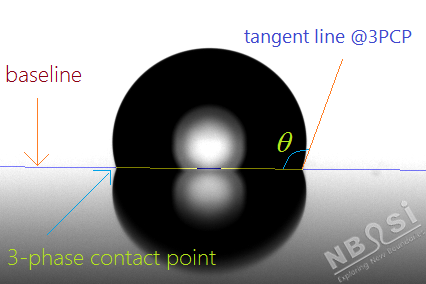图1：接触角测量示意图
除此之外，根据接触角的定义，它是在液/固/流三相接触界面处（3-phase contact points, 3PCP），液面与固体表面形成的切线角，是液面走向函数在此位置的一次导数。但实际情况是：恰巧在这一三相接触界面位置，由于各种因素的影响，液面的轮廓往往不很清晰，这就要求通过测量液面在其它位置的轮廓，并在某一模型的假设基础上，将其轮廓（走向函数）外推到三相接触界面位置，以计算出接触角，θ。这就是为什么接触角测量时必须采用一定的模型或计算方法的原因。
那么如何衡量/检测接触角测量的准确性？
如上所述，测量都是建立在某一模型的基础上，测量的准确性首先取决于采用的假设模型在多大程度上与实际被测量体系相符合的程度：符合得越好，测量的准确性也就越高。反之，即使测量的重复性再好（有些厂家甚至给出±0.01度），其数值的准确性（与真实数值的偏差）也不可能得到保证。试想一下：一种方法的误差高达10度以上，而它的测量重复性高达±0.01度，但这没有意义。
上面我们提到了视频光学法测量接触角的一个默认的前提（中心轴对称性）和必要的模型假设（液滴或液面轮廓走向函数）。采用的液滴或液面轮廓走向函数的模型与真实情况的相符合性在很大程度上直接决定了最终测量得到的接触角的准确性。
当前运用于视频光学法测量接触角的整体液滴或液面轮廓模型基本上有以下几种：
球或圆（截面）模型：如宽高法，圆法，θ/2-法等
椭球或椭圆（截面）模型：如椭圆法
Laplace-Young模型：Laplace-Young法
其中球或圆（截面）模型是假设表面张力的作用与液滴本身的重力相比，大大超过后者，所以后者的作用力可以忽略。这其实只对体积很小（小于2µl）的水滴，而且当接触角比较小时，才大致符合。对体积较大，角度较大，或非水液体，此模型的偏差相当明显，且随着体积增大，液体的密度增大，液体的表面张力减少，接触角值增大，这一偏差也将越来越大。当接触角大于120度、采用的水滴的体积在5µl以上时，偏差可超过10度以上。另外理论计算可以证明，如果采用以球或圆（截面）模型为基础的计算方法，测量得到的接触角的数值始终不可能高过约155度，不管液滴的真实接触角值其实已经远远超过这一数值。
椭球或椭圆（截面）模型是在部分考虑了液滴本身重力的影响下，液滴或液面轮廓被压扁，近似椭圆状。所以这一方法较圆法更接近真实状况，得到的接触角的值也较接近其真实值。但真的来说，当接触角的值超过90度后，其与真实状况的偏差也明显地显示出来。
当一液滴躺在一平整的固体表面上而处于力平衡（hydrostatic equilibrium）时，它的形状是由液体的表面张力、液体的体积和液体与固体表面间形成的接触角而决定的。早在100多年前Laplace和Young就先后建立了描写这一力平衡的状态方程（可以参见俯视法中的叙述：光学俯视法测量接触角以及原理），只是这一方程没有解析解。一直到最近20年，随着计算机的发展和应用，这一描写液滴轮廓的方程才得以部分求解。部分求解这一方程的前提是：液滴和液面呈现中心轴对称性。
因此对于所有符合这一前提的液滴，无论其体积、密度和接触角多大，只要其形状呈现中心轴对称性，其轮廓就可以用Laplace-Young方程得以准确描述，而且能得到求解，由此就可准确计算出其在固体表面的接触角（参见图2）。接触角的值与液滴的体积无关。
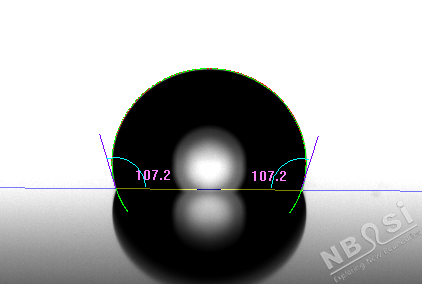图2：Laplace-Young方法计算接触角值结果
（图中的绿色曲线为根据Laplace-Young方程计算得到的最佳拟合理论曲线）
在实际测量中，有些固体表面并不完美，呈现化学（如组成、结构等）或/和物理上（如形貌，取向，应力等）的不均匀性，这一不均匀性会导致液滴和液面不再完美地呈现中心轴对称性。在这种情况下，虽然Laplace-Young方程仍可准确地描述其形状，但却无法求解。此时若仍然坚持中心轴对称性的假设前提，得到的答案会多多少少偏离真实的液滴形状，影响其最后得到的接触角值的准确性。为了更好地对付这种情况下的接触角测量的准确性，我们的软件引入了真实液滴法（TrueDrop method），它能近似地，但在多数情况下，相当准确地描述液滴的轮廓走向，而且对几乎所有的液滴形状，都能得到相当满意的结果（当然在中心轴对称性前提得以满足时，Laplace-Young法得到的结果永远是最可靠的）。
总之，要想准确测量接触角，首先要选择最接近真实液滴的模型或状态方程，在这里我们提供了当前商用仪器中最完整的多种模型选择，再加上我们引入的独特的真实液滴法。其次，选择的计算方法（模型）符合真实液滴的程度究竟有大好，可以通过观察实际测量得到的液滴轮廓线与模型拟合线之间的偏差就能很好地判断。
对于比较完美的固体表面（如许多工业制品的表面），形成的液滴基本符合中心轴对称性这一前提，此时若采用Laplace-Young法，其准确性可以达到0.1 – 0.5度（注意我们这里说的是准确性accuracy, 而非重复性或精度precision）。对于不很完美的表面，若采用适当的模型（如真实液滴法），接触角的准确性一般在0.5 - 1度左右。如果考虑到真实固体表面的不均匀性，这一准确性其实已经很高，完全可以满足各种不同的应用的要求。
影响接触角测量准确性的另一个关键因素是液滴与固体表面相接触处的基线（baseline）位置的测量（这可以从上面给出的有关接触角的定义得出）。基线位置对接触角值测量结果的影响随着接触角值的变大而迅速地增加：接触角越大，由于基线位置测定不准确而导致的接触角测量结果的误差也越大。如果测量软件没有自动、准确确定液滴基线位置的功能，基线位置只能通过肉眼观察来确定，那么其实这样的方法根本不可能达到0.1度的测量准确性，不管采用何种计算方法。而且当接触角值在90度以上时，由于基线位置误差而引起的接触角测量误差可以高达1-5度左右。
除了通常采用的基于侧面（side-view）观察法的视频光学法以外，另一种测量接触角的光学方法是采用从液滴的正上方俯视（top-view）观察液滴的形状。
© 宁波新边界科学仪器有限公司版权所有，未经许可，禁止转载。