悬滴法测量液/流-界面的界面张力
(包括液/气表面张力和液/液界面张力)

用悬滴法（Pendant Drop method）来测量液体的表面和界面张力已有很长的历史。早在19世纪初Young和Laplace先后发表了二篇有关表面张力现象和本质的文章，把表面张力，\(\gamma\)，与表面二侧的压力差，\(\Delta p\)，和表面的曲率半径，\(R_1\) 和 \(R_2\)，联系起来：

$$ \Delta p = \gamma \left( \frac{1}{R_1} + \frac{1}{R_2} \right) \tag{1} \label{1} $$

19世纪末（1882），Bashforth and Adams在杨-拉普拉斯（Young-Laplace）方程的基础上，基于中心轴对称前提，推导出了描述一处于静力（界面张力对重力）平衡时的悬滴轮廓的方程式（Eq. of Bashforth and Adams）[1]：

$$ 2 - \beta \left( \frac{z}{b} \right) = \frac{1}{R/b} + \frac{\sin\phi}{x/b} \tag{2} \label{2} $$

上式中（参见图1），\(b\) 为悬滴底端（apex）的曲率半径，\(R\) 为悬滴轮廓上一点，\(p(x, z)\)，在纸平面上的主曲率半径（principle radius of curvature），\(\phi\) 为轮廓线上点 \(p(x, z)\) 处的切线与 \(x\) 轴的夹角。 \(\beta\) 是体系的Bond number，是衡量重力相对于表面张力的影响力指数，在这里往往也被称为液滴的形状因子（shape/form parameter），因为它的数值直接决定了液滴的形状（注意：是指形状，不涉及液滴的尺寸大小）：

$$ \begin{align} \beta &= \frac{b^2\cdot\Delta\rho\cdot g}{\gamma} = \frac{b^2}{\alpha^2} \tag{3a} \\ \alpha &= \sqrt{\frac{\gamma}{\Delta\rho\cdot g}} \tag{3b} \end{align} $$

\(\Delta\rho\) 为液滴相与周围相之间的密度差；\(g\) 为重力加速度；\(\gamma\) 为表面/界面张力；\(\alpha\) 为体系的毛细管常数（capillary constant）。

从上面的方程式可以看出：一个悬滴在达到静力（界面张力对重力）平衡时，其轮廓可通过悬滴底端（apex）的曲率半径，\(b\)，和液滴的形状因子，\(\beta\)，来确定。反之也然：若能够确定 \(b\) 和 \(\beta\)，也就确定了悬滴的轮廓。

Bashforth and Adams通过对\eqref{1}式的计算制定出了相应的悬滴轮廓（的近似）数据表，并通过对真实悬滴轮廓的直接测量对获得的数据进行了检验。运用这一表格，原则上就可通过测量一悬滴的轮廓来获得液体的表/界面张力。但基于当时条件的限制，实践使用起来相当不方便。为了简化这一步骤，Andreas等 [2] 在1938年（通过对由水形成的各种形状的悬滴的直接测量）引入了经验较正因子，使得可通过测量悬滴轮廓两极限位置处的尺寸来计算出液体的表/界面张力，也即所谓的Selected-Plane Method（选择平面法或选面法）。Stauffer和Fordham [3，4] 后来通过对 Bashforth-Adams方程的求解准确地获得了这一较正因子，并列成表格。 后来Roe [5] 进一步引入多选择平面法，也即通过测量悬滴轮廓多处极限位置的特征尺寸来提高计算的可靠性和准确性。从那时起悬滴法就成为一经典的表/界面张力测量法。测量通常是通过对液滴拍照，然后通过对照片上液滴几处选择平面位置上尺寸的测量，再通过查表，就可获得表/界面张力的值（当界面两相的密度差已知时）。

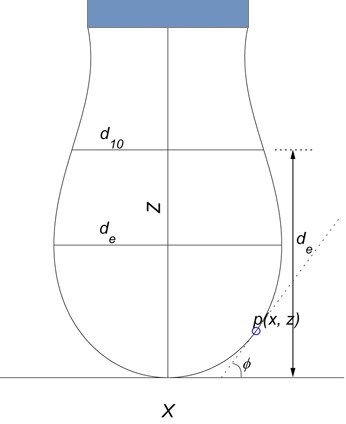悬滴示意图图1：悬滴示意图

虽然当时人们就知道悬滴法是一很可靠、准确的方法，但受当时条件的限制，使得实践操作很烦人，数据又要等到照片冲洗出来后才可获得，使得这一方法的使用不广泛，多数情况下只是局限于实验室里研究使用。

1980年代到1990年代，随着计算机技术和数字图像技术的发展，悬滴法又得到了应有的重视，并逐步被完全数字/计算机化。这不但使其成为最易于操作的测量方法，而且其测量的准确性和可靠性也获得了进一步的提高。1990年代末，首批商品化的悬滴法测量仪进入市场，从而开始了悬滴法的普遍应用阶段。

但即使引入了数字图像处理和计算机辅助，现在市场上供应的悬滴法仍可分为二类：

  1. 基于数字图像的选择平面法 （selected-plane(s) method）

  2. 基于数字图像的完整液滴轮廓法 （whole drop profile analysis）

第一种方法只是通过对获得的数字图像进行如图1所示的 \(d_e\) 和 \(d_{10}\) 的测量，再通过查表获得校正因子，从而得到液体的表/界面张力。它是“现代“的传统方法，其精度不会比从前的传统方法高，因为数字图像的坐标分辨率是有限的，而最终的表/界面张力值对 \(d_e\) 和 \(d_{10}\) 测量中的任何微小误差都很敏感（尤其对某些特定形状的悬滴）。而且这种方法的局限性也很大，因为只有呈现出 \(d_e\) （最大直径）的悬滴才可以被测量，而且当悬滴的长/宽比不是很大时，\(d_{10}/d_e\) 的比值对表面张力的值的变化不是很敏感。这种方法的精度一般很难超过2～3%，当悬滴的长/宽比接近1时（也即悬滴接近球形时）其误差更可高达20% [3]。市场上供应的有些悬滴法甚至只依靠用户的鼠标点击操作（比如所谓的5点法）来测量 \(d_e\) 和 \(d_{10}\)，这样做的最后测量结果精度一般在最好的情况下也不会高过5%，且测量结果很受主观因素以及操作者经验的影响。

SurfaceMeter™软件采用的是现代的、完全数字/计算机化的完整液滴轮廓分析悬滴法。测量过程中由一摄像机/相机抓取一悬滴的图像，并将整个图像数字化。数字化后的图像由计算机进行图像处理，测定其整个悬滴轮廓的坐标（可多至几千个坐标点），而且坐标测量可达到亚像素（sub-pixel）精度（相当于图像分辨率的成倍提高）。通过将后者拟合到描述悬滴轮廓的Bashforth-Adams方程式\eqref{2}，就可得到毛细管常数 \(\alpha\)。在知道了界面两相的密度差和重力加速度的情况下，就可由 \(\alpha\) 计算出界面的表/界面张力值（见图2）。在拟合过程中，方法不但考虑了方程中涉及的所有参数、变量，而且将几乎所有的、实际测量过程中可能存在的影响因素如图像成像过程中的可能形变、相机水平位置的可能偏差、液滴图像的可能聚焦偏差等都考虑在内。整个过程根本不需要用户任何介入，而且整个计算过程在短于一秒内就能完成，真正做到快速、准确和不受主观因素影响。而且最后的计算结果还包括液滴的质量指数，告诉用户是否有必要改变液滴的形状和尺寸，以确保测量结果的精度和准确性。这种方法的精度在一般实验条件下就可以达到约0.1%。有关方法的详细描述可参考 [7，8]。

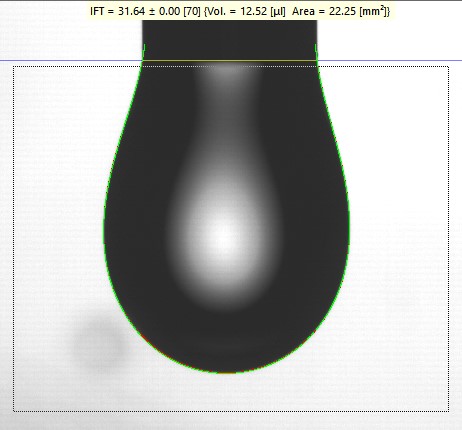悬滴图像 图像轮廓检测 图像轮廓拟合结果图2：计算过程示意图：悬滴图像（上），图像轮廓检测（中），图像轮廓拟合结果（下）；
计算结果包括界面张力及误差，液滴质量指标，液滴体积、表面积等。

悬滴法在学术界已是一公认的通用性广、可靠性高而且操作又间便的方法。与当前市场上普遍使用的一些传统测量方法（比如建立在称重原理上的吊环法或薄板法）相比，现代的全轮廓悬滴分析法几乎在所有的方面都显示出其显著的优越性。液体表/界面张力的测量方法正处于一更新换代的革新时期：在不久的将来，悬滴法终将成为最重要并被广泛使用的测量方法，而且其应用的领域也将随着研究的深入和技术的完善得以不断地扩大。在工业标准方面，2011年公布的德国技术标准DIN-55660-3已经采纳了基于悬滴法的表/界面张力测量法，目前国际标准化组织正在这一基础上制定最新的ISO测量标准（ISO/DIS 19403-3: 2015(E) draft）。

有兴趣的读者可以进一步阅读有关表/界面张力测量方法的综述章节。

光学悬滴法测量表/界面张力的特点和优点

参考文献：

  1. S. Bashforth and J. C. Adams, "An Attempt to Test the Theory of Capillary Action." Cambridge University Press and Deighton, Bell & Co., London, 1892.

  2. J. M. Andreas, E. A. Hauser, and W. B. Tucke, J. Phys. Chem., 42, 1001(1938).

  3. S. Fordham, "On the Calculation of Surface Tension from Measurements of Pendant Drops." Proc. R. Soc. London. Ser. A. A194. 1 (1948).

  4. C. E. Stauffer, "The Measurement of Surface Tension by the Pendant Drop Technique." J. Phvs. Chem., 69, 1933 (1965).

  5. R. J. Roe, V. L. Bacchetta and P. M. G. Wong, J. Phvs. Chem., 71, 4190 (1967).

  6. M. Hoorfar, A.W. Neumann, Adv. Colloid Interface Sci., 121, 25 (2006).

  7. B. Song, J. Springer, "Determination of Interfacial Tension from the Profile of a Pendant Drop Using Computer-Aided Image Processing: 1. Theoretical." J . Colloid Interface Sci., 184，64 (1996).

  8. B. Song, J. Springer, "Determination of Interfacial Tension from the Profile of a Pendant Drop Using Computer-Aided Image Processing: 2. Experimental." J . Colloid Interface Sci., 184，77 (1996).

  9. N. K. Adam. The Physics and Chemistry of Surfaces. 3rd Ed.; p. 365. Oxford University Press. 1941.

  10. J. F. Padday, "The Measurement of Surface Tension." pp. 110-12 in Surface and Colloid Science. Vol. 1. Edited by E. Matijevic, Wiley Interscience, New York, 1969.

  11. J. F. Padday, "The Profile of Axially Symmetric Menisci." Philos. Trans. R. Soc. London. Ser. A. A269. 265 (1971).

  12. J. F. Padday and A. Pitt, "Axisymmetric Meniscus Profiles." J . Colloid Interface Sci., 38, 323 (1972).

  13. P. G. de Gennes, F. Brochard-Wyart, D. Quéré, "Capillary and Wetting Phenomena — Drops, Bubbles, Pearls, Waves." Springer 2002.

© 宁波新边界科学仪器有限公司版权所有，未经许可，禁止转载。