光学俯视法接触角测量以及原理
(Determination of Contact Angle by Top-Viewing a Sessile Drop)
当对一位于固体表面上的座滴（sessile drop）从正上方朝下进行俯视观察时，可以看到，当接触角小于90°时，液滴与固体表面的三相接触周边线（3-phase contact periphery），或者，当接触角大于90°时，座滴的最大腰围周边线。从前者我们可以得到液滴在表面的接触直径（contact diameter, CD），从后者获得液滴最大腰围直径（maximum diameter, MD）。在测得了CD或MD的值后，加上一些其它的已知边界条件，就可以根据一描述座滴的模型，确定模型的所有参数，从而计算出液滴与表面接触处的接触角值。
描述座滴的模型可以是简单的球模型，或者Laplace-Young模型。前者忽略了重力对座滴形状的任何影响，把座滴看成是球体的一部分。与侧面测量计算法一样，这虽然大大简化了计算，但也同时引入了所有的由于忽略了重力影响而产生的对计算结果的影响。由于这一模型相当直观，所以这里只对Laplace-Young模型作一介绍。
早在19世纪初Young和Laplace先后发表了二篇有关表面张力现象和本质的文章，把表面张力，\(\gamma\)，与表面二侧的压力差，\(\Delta p\)，和表面的曲率半径，\(R_1\) 和 \(R_2\)，联系起来：
$$ \Delta p = \gamma \left( \frac{1}{R_1} + \frac{1}{R_2} \right) \tag{1} \label{1} $$
方程\eqref{1}看似简单，但一般情况下无法求解。19世纪末（1882），Bashforth and Adams在Young-Laplace方程的基础上，引入中心轴对称前提，推导出了描述一处于静力（表面张力对重力）平衡时的中心轴对称液滴轮廓的方程式（Eq. of Bashforth and Adams）[ 1 ]：
$$ 2 + \beta \left( \frac{z}{b} \right) = \frac{1}{R/b} + \frac{\sin\phi}{x/b} \tag{2} \label{2} $$
上式中（参见图1），\(b\) 为座滴底端 \(o\) 处（apex）的曲率半径，\(R\) 为座滴轮廓上一点，\(p(x, z)\)，在纸平面上的主曲率半径（principle radius of curvature），\(\phi\) 为轮廓线上点 \(p(x, z)\) 处的切线与 \(x\) 轴的夹角。 \(\beta\) 是体系的Bond number，是衡量重力相对于表面张力的影响力指数，在这里往往也被称为液滴的形状因子（shape/form parameter），因为它的数值直接决定了液滴的形状（注意：是指形状，不涉及液滴的尺寸大小）：
$$ \begin{align} \beta &= \frac{b^2\cdot\Delta\rho\cdot g}{\gamma} = \frac{b^2}{\alpha^2} \\ \alpha &= \sqrt{\frac{\gamma}{\Delta\rho\cdot g}} \end{align} \tag{3} \label{3} $$
\(\Delta\rho\) 为液滴相与周围相之间的密度差；\(g\) 为重力加速度；\(\gamma\) 为表面/界面张力；\(\alpha\) 为体系的毛细管常数（capillary constant）。
从上面的方程式可以看出：一个座滴在达到静力（表面张力对重力）平衡时，其轮廓可通过座滴底端（apex）的曲率半径，\(b\)，和液滴的形状因子，\(\beta\)，来确定。反之也然：若能够确定 \(b\) 和 \(\beta\)，也就确定了座滴的轮廓。
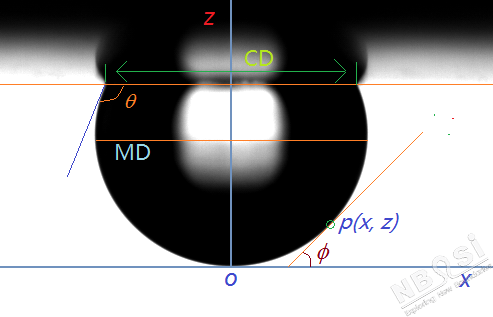图1：座滴示意图
对于一给定的测试液体，体系的毛细管常数 \(\alpha\) 是已知的。从式\eqref{3}可以得出，此时的 \(\beta\) 值直接由 \(b\) 决定。所以在这种情况下，座滴的轮廓通过单一的 \(b\) 值就能决定。而 \(b\) 值，连同液滴的高度 \(h\) （ \(h\) 是指从液滴的底端，apex，到固体表面的距离），可以进一步通过以下二个边界条件来确定：
液滴的体积 \(v\)：它是已知的输入值；
液滴的接触直径CD或最大直径MD：这个数据可以通过测量得到。
在确定了 \(b\) 值和液滴的高度后，座滴的形状也就被完全确定，而这样的解对于给定的 \(\alpha\)，\(v\)，和CD或MD组合是唯一的。在这种情况下液滴与表面形成的接触角 \(\theta\) 值就可以通过积分方程\eqref{2}直接得出。
方法的困难性在于上述的方程，即使在引入了中心轴对称的前提下，仍然只能通过数值求解，所以计算量相当大。
Laplace-Young模型由于考虑了重力的影响，所以适合任何种类的液体（也即具有不同毛细管常数 \(\alpha\) 的液体）和液滴体积 \(v\) （尺寸）。
图2：水滴（6μl）在磨砂有机玻璃表面的接触角测量：约133°
与通常的侧面测量法相比，俯视法测量接触角需要准确知道液滴的体积，而且方法对液滴体积准确性的要求随着接触角值的增大而提高。同时方法也要求准确知道测量仪器的光学放大倍数，以准确测量液滴接触直径CD或最大直径MD的绝对数值。
与通常的侧面测量法相比，俯视接触角测量法具有许多显著的特点和优点，具体可参看：
OSA™ Optical Surface Analyzer - SKX系列
参考文献：
S. Bashforth and J. C. Adams, An Attempt to Test the Theory of Capillary Action, Cambridge University Press and Deighton, Bell & Co., London, 1892.
F.K. Skinner, Y. Rotenberg and A.W. Neumann, J. Colloid Interface Sci., 130, 25 (1989).
E. Moy, P. Cheng, Z. Policova, S. Treppo, D. Kwok, D.P. Mack, P.M. Sherman, A.W. Neumann，Colloids and Surfaces, 58, 215 (1991).
© 宁波新边界科学仪器有限公司版权所有，未经许可，禁止转载。